Ley de Wiedemann franz

Ley de Wiedemann franz

La ley de Wiedemann-Franz establece que en el caso de metales a temperaturas no demasiado bajas el cociente entre la conductividad térmica y la eléctrica es directamente proporcional a la temperatura, siendo el valor de la constante de proporcionalidad independiente del metal en particular se define el numero de lorenz L=2.45e−8 W/K2

La razón de la conductividad calorífica K a la conductividad eléctrica para la mayoría de los metales es proporcional a la temperatura T, siendo el factor de proporcionalidad L igual para todos los metales:

K/ =L*T

Esto es debido a que se supone que la parte más importante del flujo calorífico, cuando existe gradiente de temperatura T, es transportada por los electrones de conducción. El metal puede representarse en forma de una caja llena de electrones libres para los cuales son válidas las leyes de la teoría cinética de los gases. Para que el metal fuera eléctricamente neutro se consideraba que contenía también la cantidad correspondiente de partículas más pesadas (iones), cargadas positivamente, en reposo. Se suponía también que los electrones estaban distribuidos según la función de distribución de Fermi−Dirac:

f=(m/h)3 1/4_(exp[mv −Ep/KbT]+1)

En la que m es la masa de los electrones y v su velocidad.

De acuerdo con esta distribución, los electrones tienen a la temperatura T todos los valores posibles de las velocidades, con la particularidad de que, en ausencia de fuerzas exteriores, todas las direcciones de las velocidades son equiprobables y varían continuamente a causa de los choques con las partículas cargadas positivamente. No tendremos en cuenta las interacciones de un electrón con los otros en los intervalos entre choques.

Para calcular la conductividad eléctrica vamos a suponer que durante el tiempo unidad un electrón experimenta choques con una probabilidad de 1/ donde es el tiempo de relajación o tiempo de recorrido libre del electrón. En cada choque el electrón sólo varía la dirección de su velocidad. En el tiempo el electrón recorre la distancia entre dos choques, igual al recorrido libre medio:

<>=v

Si los extremos opuestos del metal se someten a una diferencia de potencial que cree en cada punto del metal un campo eléctrico de intensidad E, el electrón, bajo la acción de una fuerza F=eE tendrá entre dos choques un movimiento uniformemente acelerado. Después de cada choque la velocidad del electrón puede tener cualquier dirección, con lo que la aportación a la velocidad media en la dirección del campo es:

=(eE/m)

En la realidad la relación K/ resulta ser una magnitud constante sólo a temperatura ambiente y a temperaturas más altas no depende de la clase de metal ni de T. En la región intermedia esta relación depende de la clase de metal y de la temperatura, ya que la conductividad calorífica en esta región no varía tan deprisa como puede esperarse por la ley de Wiedeman−Franz. La desviación de la ley de Wiedeman−Franz se debe a que el recorrido libre medio correspondiente a la conductividad eléctrica y calorífica, en general, son distintos, y no iguales como se supone en la teoría. Son iguales con exactitud bastante grande únicamente a temperaturas altas.

El comportamiento de la conductividad calorífica es el siguiente:

K=nKb< >T/3mvf

En la fórmula anterior sólo depende de T el recorrido libre medio, que viene determinado por la dispersión de los electrones en los fonones y disminuye cuanto más denso es el gas fonónico.

A temperaturas altas (T>> h) el tiempo de relajación va como 1/T y por tanto también. Por consiguiente,

K=cte, es decir, la conductividad calorífica no depende de la temperatura.

A temperaturas bajas (T<

A temperaturas más bajas, próximas a 0K, la conductividad calorífica es proporcional a la capacidad calorífica del gas electrónico, o sea, a T.

En la gráfica se observa el comportamiento de la conductividad, tal y como acabamos de describir.

Podríamos haber considerado también la conductividad calorífica condicionada por los fonones, pero es de la orden de 102 veces más pequeña y la despreciamos frente a la de los electrones.

La teoría de Sommerfeld de la conducción eléctrica y térmica

Los cuerpos de algunas sustancias tienen la propiedad de conducir el calor o la electricidad. Los que tienen esa propiedad se llaman conductores; los que no, aisladores. Estas propiedades son mensurables y sus medidas se llaman, respectivamente, conductividad eléctrica y conductividad térmica.

En los primeros esfuerzos por explicar la estructura electrónica de los metales, los científicos esgrimieron las propiedades de la buena conductividad térmica y eléctrica para apoyar la teoría de que los metales se componen de átomos ionizados, cuyos electrones libres forman un "mar" homogéneo de carga negativa.

La atracción electrostática entre los iones positivos del metal y los electrones libres, se consideró la responsable del enlace entre los átomos del metal. Así, se pensaba que el libre movimiento de los electrones era la causa de su alta conductividad eléctrica y térmica. La principal objeción a esta teoría es que en tal caso los metales debían tener un calor específico superior al que realmente tienen.

En 1928, el físico alemán Arnold Sommerfeld sugirió que los electrones en los metales se encuentran en una disposición cuántica en la que los niveles de baja energía disponibles para los electrones se hallan casi completamente ocupados.

En el mismo año, el físico suizo estadounidense Félix Bloch, y más tarde el físico francés Louis Brillouin, aplicaron esta idea en la hoy aceptada "teoría de la banda" para los enlaces en los sólidos metálicos.

De acuerdo con dicha teoría, todo átomo de metal tiene únicamente un número limitado de electrones de valencia con los que se unen a los átomos vecinos. Por ello se requiere un amplio reparto de electrones entre los átomos individuales. El reparto de electrones se consigue por la superposición de orbitales atómicos de energía equivalente con los átomos adyacentes.
La teoría de Sommerfeld de la conducción eléctrica y térmica Los cuerpos de algunas sustancias tienen la propiedad de conducir el calor o la electricidad. Los que tienen esa propiedad se llaman conductores; los que no, aisladores. Estas propiedades son mensurables y sus medidas se llaman, respectivamente, conductividad eléctrica y conductividad térmica.

En los primeros esfuerzos por explicar la estructura electrónica de los metales, los científicos esgrimieron las propiedades de la buena conductividad térmica y eléctrica para apoyar la teoría de que los metales se componen de átomos ionizados, cuyos electrones libres forman un "mar" homogéneo de carga negativa.

La atracción electrostática entre los iones positivos del metal y los electrones libres, se consideró la responsable del enlace entre los átomos del metal. Así, se pensaba que el libre movimiento de los electrones era la causa de su alta conductividad eléctrica y térmica. La principal objeción a esta teoría es que en tal caso los metales debían tener un calor específico superior al que realmente tienen.

En 1928, el físico alemán Arnold Sommerfeld sugirió que los electrones en los metales se encuentran en una disposición cuántica en la que los niveles de baja energía disponibles para los electrones se hallan casi completamente ocupados.

En el mismo año, el físico suizo estadounidense Félix Bloch, y más tarde el físico francés Louis Brillouin, aplicaron esta idea en la hoy aceptada "teoría de la banda" para los enlaces en los sólidos metálicos.

De acuerdo con dicha teoría, todo átomo de metal tiene únicamente un número limitado de electrones de valencia con los que se unen a los átomos vecinos. Por ello se requiere un amplio reparto de electrones entre los átomos individuales. El reparto de electrones se consigue por la superposición de orbitales atómicos de energía equivalente con los átomos adyacentes.

La conductividad termica

El método de Hartree-Fock

El método de Hartree-Fock (HF) es una forma aproximada de las ecuaciones de mecánica cuántica para fermiones, utilizada en física y química (donde también se conoce como método de campo auto consistente). Esto se debe a que sus ecuaciones, basadas en orbitales de una partícula, son más accesibles computacionalmente que los métodos basados en funciones de onda de muchas partículas.

La aproximación de Hartree-Fock es el equivalente, en física computacional, a la aproximación de orbitales moleculares, de enorme utilidad conceptual para los físicos. Este esquema de cálculo es un procedimiento iterativo para calcular la mejor solución monodeterminantal a la ecuación de Schrödinger independiente del tiempo, para moléculas aisladas, tanto en su estado fundamental como en estado excitados. La interacción de un único electrón en un problema de muchos cuerpos con el resto de los electrones del sistema se aproxima promediándolo como una interacción entre dos cuerpos (tras aplicar la aproximación de Born-Oppenheimer). De esta forma, se puede obtener una aproximación a la energía total de la molécula. Como consecuencia, calcula la energía de intercambio de forma exacta, pero no tiene en absoluto en cuenta el efecto de la correlación electrónica.

La base del método de Hartree-Fock es suponer que la función de onda de muchos cuerpos es un determinante de Slater de orbitales de una partícula. Esto garantiza la antisimetría de la función de onda y considera la energía de intercambio. Sin embargo, no considera efectos de correlación que no necesariamente son despreciables. A partir de esta suposición, se puede aplicar el principio variacional de mecánica cuántica, se encuentra una ecuación de autovalores para los orbitales de una partícula.

El punto de partida para el cálculo Hartree-Fock es un conjunto de orbitales aproximados. Para un cálculo atómico, estos son típicamente los orbitales de un átomo hidrogenoide (un átomo con una carga nuclear cualquiera pero con un sólo electrón). Para cálculos moleculares o cristalinos, las funciones de ondas iníciales son típicamente una combinación lineal de orbitales atómicos. Esto da una colección de orbitales monoelectrónicos, que por la naturaleza fermiónica de los electrones, debe ser antisimétrica, lo que se consigue mediante el uso del determinante de Slater. El procedimiento básico fue diseñado por Hartree, y Fock añadió el antisimetrizado.

Una vez se ha construido una función de ondas inicial, se elige un electrón. Se resume el efecto de todos los demás electrones, que se usa para generar un potencial. (Por este motivo, se llama a veces a este método un procedimiento de campo promedio). Esto da un electrón en un campo definido, para el que se puede resolver la ecuación de Schrödinger, dando una función de ondas ligeramente diferente para este electrón. Entonces, el procedimiento se repite para cada uno de los otros electrones, hasta completar un paso del procedimiento. De esta forma, con la nueva distribución electrónica se tiene un nuevo potencial eléctrico. El procedimiento se repite, hasta alcanzar la convergencia (hasta que el cambio entre un paso y el siguiente es lo suficientemente pequeño

Las aplicaciones del método de Hartree-Fock Se usa a menudo en el mismo área de cálculos que la Teoría del Funcional de la Densidad, que puede dar soluciones aproximadas para las energías de canje y de correlación. De hecho, es común el uso de cálculos que son híbridos de los dos métodos. Adicionalmente, los cálculos a nivel Hartree-Fock se usan como punto de partida para métodos más sofisticados, como la teoría perturbacional de muchos cuerpos, o cálculos cuánticos de Monte-Carlo.

La inestabilidad numérica es un problema de este método, y hay varias vías para combatirla. Una de las más básicas y más aplicadas es la mezcla-F. Con la mezcla-F, no se usa directamente la función de ondas de un electrón conforme se ha obtenido. En lugar de esto, se usa una combinación lineal de la función obtenida con las previas, por ejemplo con la inmediatamente previa. Otro truco, empleado por Hartree, es aumentar la carga nuclear para comprimir a los electrones; tras la estabilización del sistema, se reduce gradualmente la carga hasta llegar a la carga correcta.

Desarrollos más allá del campo autoconsistente o SCF son el CASSCF y la interacción de configuraciones. Los cálculos de este tipo son relativamente económicos frente a otros de la química cuántica. De esta forma, en ordenadores personales es posible resolver moléculas pequeñas en muy poco tiempo. Las moléculas más grandes, o los desarrollos más sofisticados, para obtener resultados más exactos, siguen realizándose en superordenadores. Existen múltiples paquetes informáticos que implementan el método de campo autoconsistente, entre los que pueden destacarse Gaussian, MOLPRO y MOLCAS.

Fisica de la materia condensada, introducción general

La Física de la Materia Condensada es el campo de la física que se ocupa de las características físicas macroscópicas de la materia. En particular, se refiere a las fases "condensadas" que aparecen siempre que el número de constituyentes en un sistema sea extremadamente grande y que las interacciones entre los componentes sean fuertes. Los ejemplos más familiares de fases condensadas son los sólidos y los líquidos, que surgen a partir de los enlaces y uniones causados por interacciones electromagnéticas entre los átomos. Entre las fases condensadas más exóticas se cuentan las fases superfluidas y el condensado de Bose-Einstein, que se encuentran en ciertos sistemas atómicos sometidos a temperaturas extremadamente bajas, la fase superconductora exhibida por los electrones de la conducción en ciertos materiales, y las fases ferromagnética y antiferromagnética de espines en redes atómicas.

La Física de la Materia Condensada es, por lejos, el campo más extenso de la física contemporánea. Un enorme progreso ha sido realizado en la rama teórica de la física de la materia condensada. Para una estimación, un tercio de todos los físicos americanos se identifica a sí mismo como físicos trabajando en temas de la materia condensada. Históricamente, dicho campo nació a partir de la física del estado sólido, que ahora es considerado como uno de sus subcampos principales. El término "física condensada de la materia" fue acuñado, al parecer, por Philip Anderson, cuando renombró a su grupo de investigación - previamente "teoría del estado sólido" - (1967). En 1978, la División de Física del Estado Sólido de la American Physical Society fue renombrada como División de Física de Materia Condensada. El campo de estudio de la física de la materia condensada tiene una gran superposición con áreas de estudio de la química, la ciencia de materiales, la nanotecnología y la ingeniería.

Una de las razones para que la "física de materia condensada" reciba tal nombre es que muchos de los conceptos y técnicas desarrollados para estudiar sólidos se aplican también a sistemas fluidos. Por ejemplo, los electrones de conducción en un conductor eléctrico forman un tipo de líquido cuántico que tiene esencialmente las mismas características que un fluido conformado por átomos. De hecho, el fenómeno de la superconductividad, en el cual los electrones se condensan en una nueva fase fluida en la cual puedan fluir sin disipación, presenta una gran analogía con la fase superfluida que se encuentra en el helio-3 a muy bajas temperaturas.

Un sólido cristalino es aquél que tiene una estructura periódica y ordenada, como consecuencia tienen una forma que no cambia, salvo por la acción de fuerzas externas. Cuando se aumenta la temperatura, los sólidos se funden y cambian al estado líquido. Las moléculas ya no permanecen en posiciones fijas, aunque las interacciones entre ellas sigue siendo suficientemente grande para que el líquido pueda cambiar de forma sin cambiar apreciablemente de volumen, adaptándose al recipiente que lo contiene.

sólido amorfo es a sólido en cuál allí es no orden de largo alcance de las posiciones del átomos. (Los sólidos en que allí son orden atómica de largo alcance se llaman sólidos cristalinos o morphous). La mayoría de las clases de materiales sólidos se pueden encontrar o preparar en una forma amorfa. Por ejemplo, ventana común cristal es un amorfo de cerámica, muchos polímeros (por ejemplo poliestireno) son los alimentos amorfos, y uniformes por ejemplo caramelo de algodón son los sólidos amorfos.

En el principio, dado una tarifa que se refresca suficientemente alta, cualquier líquido se puede hacer en un sólido amorfo. El refrescarse reduce movilidad molecular. Si la tarifa que se refresca es más rápida que la tarifa en la cual las moléculas pueden organizar en más termodinámico el estado cristalino favorable, entonces un sólido amorfo será formado. Debido a consideraciones de la entropía, muchos polímeros se pueden hacer los sólidos amorfos refrescándose incluso en las tarifas lentas. En cambio, si las moléculas tienen suficiente tiempo para organizar en una estructura con dos u orden tridimensional, entonces un sólido cristalino (o semi-cristalino) será formado. El agua es un ejemplo. Debido a su tamaño y capacidad moleculares pequeños de cambiar rápidamente, no puede ser hecho amorfo sin el recurso a las técnicas hyperquenching especializadas.

Los materiales amorfos se pueden también producir por los añadidos que interfieren con la capacidad del componente primario de cristalizarse. Por ejemplo, adición de soda a dióxido del silicio resultados en cristal de la ventana, y la adición de glicoles a agua resultados en a vitrified sólido.

Los cristales líquidos son apreciados por sus singulares propiedades ópticas y de autorreparación. Generalmente consisten en moléculas de formas especiales que se alinean en el estado líquido por su forma. Usando campos eléctricos para manipular la orientación de las moléculas de cristal líquido, los científicos pueden controlar si la luz puede o no atravesar el material líquido cristalino. Sin los cristales líquidos, artículos que consideramos cotidianos como las pantallas planas de numerosos aparatos, o los relojes con display LCD, no existirían.

Los cristales líquidos más conocidos son moléculas orgánicas compuestas de carbono, nitrógeno y oxígeno. Agregar materiales inorgánicos, o metales, a estos cristales líquidos para acceder a sus propiedades eléctricas o magnéticas era problemático porque la estructura de estas moléculas hace difícil lograr las altas concentraciones metálicas necesarias para que sean útiles.

Conducción Eléctrica De Los Materiales : No todos los materiales conducen la electricidad de la misma forma. Para diferenciarlos, decimos que algunos presentan mayor "resistencia" que otros a conducir la electricidad.

La resistencia eléctrica es una medida cuantitativa respecto de cuán buen conductor es un material. La resistencia eléctrica se mide en ohmios, en honor a Georg Simon Ohm (1787-1854), que desarrolló los principios agrupados en la ley de Ohm (ver recuadro). A los materiales que presentan baja resistencia eléctrica se les llama buenos conductores eléctricos. A su vez, a aquellos que poseen alta resistencia eléctrica se les denomina malos conductores eléctricos. Cambios en la resistencia ¿Qué puede hacer cambiar la resistencia eléctrica en un material conductor? Volvamos a nuestro modelo del "juego de las manzanas verdes". Si permitimos que más individuos se incorporen al juego y, de este modo, aumentamos la longitud del grupo en relación al campo de juego, ¿qué sucederá con la conducción de las manzanas? Pues bien, dado que ahora existe una mayor cantidad de individuos a través de los cuales debe pasar cada manzana, observaremos que la conducción cambia. Esto, pues habiendo una mayor cantidad de personas, aumenta el número de manzanas que se caen al suelo, o bien el número de ellas que son mordisqueadas, lo que trae como consecuencia que la conducción empeore.

Por otra parte, si en vez de aumentar la longitud del grupo, aumentamos el espacio por donde pasarán las manzanas es decir, aumentamos el ancho, incorporando más jugadores distribuidos en el campo de juego, también observaremos que la conducción cambia. Puesto que, si bien en este caso, al aumentar la cantidad de individuos, es mayor la cantidad de manzanas que se caen al suelo o son mordisqueadas, a su vez es mayor también la cantidad de manzanas que circulan por el grupo, dado que al aumentar el ancho de este hay más personas sacando manzanas desde los cajones, con lo cual observaremos -contrario al caso anterior, donde solo saca manzanas quien está al comienzo de la fila de jugadores que la conducción de manzanas mejora.

Análogamente a nuestro modelo, en un material conductor la resistencia eléctrica aumenta mientras mayor sea el largo del conductor por el cual circula una corriente, y disminuye cuando aumenta el área de este.

La respuesta dielectrica: Se denomina dieléctricos a los materiales que no conducen la electricidad, por lo se pueden utilizar como aislantes eléctricos.

Algunos ejemplos de este tipo de materiales son el vidrio, la cerámica, la goma, la mica, la cera, el papel, la madera seca, la porcelana, algunas grasas para uso industrial y electrónico y la baquelita. Los dieléctricos se utilizan en la fabricación de condensadores, para que las cargas reaccionen. Cada material dieléctrico posee una constante dieléctrica k. que es conocida como la constante de proporcionalidad directa e inversamente proporcional hablando matematicamente

Tenemos k para los siguiente dieléctricos: vacío tiene k = 1; aire (seco) tiene k = 1,00059; teflón tiene k = 2,1; nylon tiene k = 3,4; papel tiene k = 3,7; agua tiene k = 80.

Los dieléctricos más utilizados son el aire, el papel y la goma.

El magnetismo es un fenómeno físico por el que los materiales ejercen fuerzas de atracción o repulsión sobre otros materiales. Hay algunos materiales conocidos que han presentado propiedades magnéticas detectables fácilmente como el níquel, hierro, cobalto y sus aleaciones que comúnmente se llaman imanes. Sin embargo todos los materiales son influenciados, de mayor o menor forma, por la presencia de un campo magnético.

También el magnetismo tiene otras manifestaciones en física, particularmente como uno de los dos componentes de la onda electromagnética, como, por ejemplo, la luz.

Expansión térmica: La mayoría de los sólidos se expanden cuando se calientan y se contraen cuando se enfrían.

Esta es una propiedad del material que es indicativa de la magnitud a la cual un material se expande bajo calentamiento y tiene unidades de temperatura recíproca (ºC)-1 ó (ºF)-1. Por supuesto el calentamiento ó el enfriamiento afecta toda las dimensiones de un cuerpo con un cambio en el volumen resultante.Desde el punto de vista atómico la expansión térmica se refleja por un incremento en el promedio de la distancia entre los átomos . Este fenómeno se puede entender mejor observando la curva de energía potencial versus espaciamiento interatómico para un material sólido.

Teorema de bloch, Distribución de fermi, densidad de estados

Teorema de Bloch:

Picard demostró (en 1879) que las funciones enteras no constantes tienen la

propiedad de tomar todos los valores del plano complejo salvo, eventualmente,

uno de ellos. Su demostración se ha ido simpli.cando con el tiempo; el primero

en hacerla más sencilla fue Bloch (1925). Las restricciones que aparecen en

el enunciado corresponden, como se comprobará después de su demostración,

a meras normalizaciones. (Y dicho sea de paso, no hay la más mínima idea

subyacente en esta demostración de cuáles son sus claves.)

Distribución de Fermi

La estadística de Fermi-Dirac es la forma de contar estados de ocupación de forma estadística en un sistema de fermiones. Forma parte de la Mecánica Estadística. Y tiene aplicacines sobre todo en la Física del estado sólido.

Donde

n_i el número promedio de partículas en el estado de energía ε_i.

g_i es la degeneración el estado i-ésimo

ε_i es la energía en el estado i-ésimo

μ es el potencial químico

T es la temperatura

k_B la constante de Boltzmann

Interpretación Física
Para bajas temperaturas, la distribución de fermi es una función escalón que vale 1 si ε < μ y 0 si ε > μ. Esto quiere decir que las partículas van colocando desde el nivel más bajo de energía hacia arriba debido al Principio de exclusión de Pauli hasta que se hayan puesto todas las partículas. La energía del último nivel ocupado se denomina energía de Fermi y la temperatura a la que corresponde esta energía mediante εf = kBTf temperatura de Fermi.
Se da la circunstancia de que la temperatura de Fermi de la mayoría de metales reales es enorme (del orden de 10000 Kelvin), por tanto la aproximación de decir que la distribución de Fermi-Dirac sigue siendo un escalón hasta temperatura ambiente es válida con bastante precisión.
La distribución de Fermi-Dirac tiene importancia capital en el estudio de gases de fermiones y en particular en el estudio de los electrones libres en un metal.

La superficie de Fermi del electrón libre
a) La interacción del electrón con el potencial periódico del cristal causa la aparición de saltos de energía en las fronteras de zona
b) La superficie de Fermi interseca las fronteras de zona perpendicularmente
c) El potencial cristalino redondea las esquinas puntiagudas en las superficies de Fermi
d) El volumen total encerrado por la superficie de Fermi depende solo de la concentración electrónica y no de los detalles de la interacción con la red

La densidad de estados:

La Teoría del Funcional de la Densidad (DFT en sus siglas en inglés) es una formulación alternativa de la mecánica cuántica en la que la magnitud básica es la densidad y no la función de ondas de las sustancias. La ventaja es que la densidad es una magnitud mucho más simple que dicha función de ondas y por lo tanto más fácil de calcular. La desventaja es que no se conocen de manera exacta las ecuaciones de la teoría del funcional de la densidad y debemos aproximarlas.

Se aplica principalmente a la descripción del comportamiento de los electrones tanto en química como en física de la materia condensada, donde el objeto central es la densidad electrónica. Aunque también ha sido aplicada a otras áreas como la física nuclear.

La Teoría del Funcional de la Densidad (DFT en sus siglas en inglés) es una formulación alternativa de la mecánica cuántica en la que la magnitud básica es la densidad y no la función de ondas de las sustancias. La ventaja es que la densidad es una magnitud mucho más simple que dicha función de ondas y por lo tanto más fácil de calcular. La desventaja es que no se conocen de manera exacta las ecuaciones de la teoría del funcional de la densidad y debemos aproximarlas.

Se aplica principalmente a la descripción del comportamiento de los electrones tanto en química como en física de la materia condensada, donde el objeto central es la densidad electrónica. Aunque también ha sido aplicada a otras áreas como la física nuclear.

Teoria de Sommerfeld, modelo de electrones libres, conductividad electrica.

En 1916, Sommerfeld perfeccionó el modelo atómico de Bohr intentando paliar los dos principales defectos de éste. Para eso introdujo dos modificaciones básicas: Órbitas cuasi-elípticas para los electrones y velocidades relativistas. En el modelo de Bohr los electrones sólo giraban en órbitas circulares. La excentricidad de la órbita dio lugar a un nuevo número cuántico: el número cuántico azimutal, que determina la forma de los orbitales, se lo representa con la letra l y toma valores que van desde 0 hasta n-1. Las órbitas con:

* l = 0 se denominarían posteriormente orbitales s o sharp

* l = 1 se denominarían 2 p o principal.

* l = 2 se denominarían d o diffuse.

* l = 3 se denominarían f o fundamental.

Para hacer coincidir las frecuencias calculadas con las experimentales, Sommerfeld postuló que el núcleo del átomo no permanece inmóvil, sino que tanto el núcleo como el electrón se mueven alrededor del centro de masas del sistema, que estará situado muy próximo al núcleo al tener este una masa varios miles de veces superior a la masa del electrón.

Para explicar el desdoblamiento de las líneas espectrales, observando al emplear espectroscopios de mejor calidad, Sommerfeld supone que las órbitas del electrón pueden ser circulares y elípticas. Introduce el número cuántico secundario o azimutal, en la actualidad llamado l, que tiene los valores 0, 1, 2,…(n-1), e indica el momento angular del electrón en la órbita en unidades de \frac {h}{2\pi}, determinando los subniveles de energía en cada nivel cuántico y la excentricidad de la órbita.

Modelo de electrones libres:

En la física del estado sólido, el modelo de electrones libres es un modelo simple para el comportamiento de los electrones de valencia en una estructura cristalina de un sólido metálico. It was developed principally by Arnold Sommerfeld who combined the classical Drude model with quantum mechanical Fermi-Dirac statistics . Fue desarrollado principalmente por Arnold Sommerfeld, quien combinó el modelo de Drude clásica con cuántica de Fermi mecánica-Dirac. Given its simplicity, it is surprisingly successful in explaining many experimental phenomena, especially Habida cuenta de su sencillez, es un éxito sorprendente para explicar muchos fenómenos experimentales, sobre todo

* la Ley de Wiedemann-Franz que se refiere la conductividad eléctrica y la conductividad térmica.

* la dependencia de la temperatura de la capacidad calorífica.

* la forma de la densidad electrónica de los Estados.

* el rango de valores de energía de enlace.

* conductividad eléctrica.

La asunción de los electrones que se mueven libremente a través de un potencial periódico debe compararse con el modelo ajustado de unión, que utiliza la simplificación del tratamiento frente a los electrones fuertemente ligados a los núcleos atómicos. (Coulomb interactions between electrons are still neglected.) The predictions of these two complementary models are reassuringly similar. (Interacciones de Coulomb entre los electrones siguen desatendidas.) Las predicciones de estos dos modelos complementarios son la warfarina. Taking into account the specificities of the potential in a real, three-dimensional crystal lattice leads to more complicated dispersion relations and to band theory . Teniendo en cuenta las especificidades de las posibilidades de una verdadera red cristalina de tres dimensiones conduce a una mayor dispersión de las relaciones complicadas y de la teoría de la banda. In fact, the Bethe-Sommerfeld theory generalizes the thermodynamics of free-electron systems also in these respects. De hecho, la teoría de Bethe-Sommerfeld, generaliza la termodinámica de los sistemast de electrones libres, también en estos aspectos.

Propiedades transporte metal en un semiconductor

Propiedades de transporte
Al separar dos átomos (de carga n) considerablemente no interactúan entre sí y sus niveles de energía se pueden considerar casi nulos, o sea, como aislados pero al juntar estos dos átomos, sus órbitas exteriores empezaran a traslaparse y al llegar a una interacción bastante intensa forman dos niveles diferentes (n). Al realizar esto con un gran número de átomos ocurre algo similar. Conforme los átomos se acercan unos a otros, los diversos niveles de energía atómicos empiezan a dividirse. A esta división es a lo que podemos llamar una Banda, y el ancho de esta banda de energía que surge de un nivel de energía atómica particular es independiente del número de átomos en un sólido. El ancho de una banda de energía depende sólo de las interacciones de vecinos cercanos, en tanto que el número de niveles dentro de la banda depende del número total de partículas interactuando.
En otras palabras seria lo mismo decir que los electrones pueden ocupar un número discreto de niveles de energía, pueden tener solamente aquellas energías que caen dentro de las bandas permitidas. La banda donde se mueven normalmente los electrones de valencia se conoce como banda de valencia, y los electrones que se mueven libremente y conducen la corriente se mueven en la banda de conducción.

Un semiconductor es una sustancia que se comporta como conductor o como aislante dependiendo de la temperatura del ambiente en el que se encuentre.
Semiconductor intrínseco Un cristal de silicio forma una estructura tetraédrica similar a la del carbono mediante enlaces covalentes entre sus átomos, en la figura representados en el plano por simplicidad. Cuando el cristal se encuentra a temperatura ambiente, algunos electrones pueden, absorbiendo la energía necesaria, saltar a la banda de conducción, dejando el correspondiente hueco en la banda de valencia (1). Las energías requeridas, a temperatura ambiente son de 1,12 y 0,67 eV para el silicio y el germanio respectivamente.
Obviamente el proceso inverso también se produce, de modo que los electrones pueden caer desde el estado energético correspondiente a la banda de conducción, a un hueco en la banda de valencia liberando energía. A este fenómeno, se le denomina recombinación. Sucede que, a una determinada temperatura, las velocidades de creación de pares e-h, y de recombinación se igualan, de modo que la concentración global de electrones y huecos permanece invariable. Siendo "n" la concentración de electrones (cargas negativas) y "p" la concentración de huecos (cargas positivas), se cumple que:
ni = n = p
siendo ni la concentración intrínseca del semiconductor, función exclusiva de la temperatura. Si se somete el cristal a una diferencia de tensión, se producen dos corrientes eléctricas. Por un lado la debida al movimiento de los electrones libres de la banda de conducción, y por otro, la debida al desplazamiento de los electrones en la banda de valencia, que tenderán a saltar a los huecos próximos (2), originando una corriente de huecos en la dirección contraria al campo eléctrico cuya velocidad y magnitud es muy inferior a la de la banda de conducción.
Semiconductor extrínseco Si a un semiconductor intrínseco, como el anterior, se le añade un pequeño porcentaje de impurezas, es decir, elementos trivalentes o pentavalentes, el semiconductor se denomina extrínseco, y se dice que está dopado. Evidentemente, las impurezas deberán formar parte de la estructura cristalina sustituyendo al correspondiente átomo de silicio.
Aislantes.
La magnitud de la banda prohibida es muy grande ( 6 eV ), de forma que todos los electrones del cristal se encuentran en la banda de valencia incluso a altas temperaturas por lo que, al no existir portadores de carga libres, la conductividad eléctrica del cristal es nula.
Un ejemplo es el diamante
La superconductividad ocurre en una gran variedad de materiales, incluyendo elementos simples como el estaño y el aluminio, diversas aleaciones metálicas y algunos semiconductores fuertemente dopados. La superconductividad no ocurre en metales nobles como el oro y la plata, ni en la mayoría de los metales ferromagnéticos.
La teoría de Drude de los metales Esta relacionado con las propiedades físicas de los metales, por lo que comenzaremos hablando un poco sobre estos mismos para así poder comprender mejor lo que es el mar de Drude.
La ciencia de materiales define un metal como un material en el que existe un traslape entre la banda de valencia y la banda de conducción en su estructura electrónica (enlace metálico). Esto le da la capacidad de conducir fácilmente calor y electricidad, y generalmente la capacidad de reflejar la luz, lo cual le da su peculiar brillo.
Los metales tienen ciertas propiedades físicas características: a excepción del mercurio son sólidos a condiciones ambientales normales, suelen ser opacos y brillantes, tener alta densidad, ser dúctiles y maleables, tener un punto de fusión alto, ser duros, y ser buenos conductores del calor y electricidad. Estas propiedades se deben al hecho de que los electrones exteriores están ligados sólo ligeramente a los átomos, formando una especie de mar (también conocido como mar de Drude), que se conoce como Enlace metálico.
Mediante la teoría del mar de Drude podemos explicar por que los metales son tan buenos conductores del calor y la electricidad, es necesario comprender la naturaleza del enlace entre sus átomos.
Un primer intento para explicar el enlace metálico consistió en considerar un modelo en el cual los electrones de valencia de cada metal se podían mover libremente en la red cristalina (teoría de Drude-Lorentz); de esta forma, el retículo metálico se considera constituido por un conjunto de iones positivos (los núcleos rodeados por su capa de electrones) y electrones (los de valencia), en lugar de estar formados por átomos neutros.
En definitiva un elemento metálico se considera que esta constituido por cationes metálicos distribuidos regularmente e inmersos en un “mar de electrones” de valencia deslocalizados, actuando como un aglutinante electrostática que mantiene unidos a los cationes metálicos.
El modelo de mar de electrones permite una explicación cualitativa sencilla de la conductividad eléctrica y térmica de los metales. Dado que los electrones son móviles, se puede trasladar desde el electrodo negativo al positivo cuando el metal se somete al efecto de un potencial eléctrico. Los electrones móviles también pueden conducir el calor transportando la energía cinética de una parte a otra del cristal. El carácter dúctil y maleable de los metales está permitido por el hecho de que el enlace deslocalizado se extiende en todas las direcciones; es decir, no está limitado a una orientación determinada, como sucede en el caso de los sólidos de redes covalentes.
Cuando un cristal metálico se deforma, no se rompen enlaces localizados; en su lugar, el mar de electrones simplemente se adapta a la nueva distribución de los cationes, siendo la energía de la estructura deformada similar a la original. La energía necesaria para deformar un metal como el Litio es relativamente baja, siendo, como es lógico, mucho mayor la que se necesita para deformar un metal de transición, por que este último posee muchos más electrones de valencia que son el aglutinante electrostático de los cationes.
Mediante la teoría del mar de electrones se pueden justificar de forma satisfactoria muchas propiedades de los metales, pero no es adecuada para explicar otros aspectos, como la descripción detallada de la variación de la conductividad entre los elementos metálico

Superficie de fermi

La Superficie de Fermi es la energía del nivel más alto ocupado por un sistema cuántico a temperatura cero (0 K). Se denota por EF y recibe su nombre del físico italo-americano Enrico Fermi.
La energía de Fermi es importante a la hora de entender el comportamiento de partículas fermiónicas, como por ejemplo los electrones. Los fermiones son partículas de spin semientero que verifican el Principio de exclusión de Pauli que dicta que dos fermiones no pueden ocupar simultáneamente el mismo estado cuántico. De esta manera, cuando un sistema posee varios electrones, estos ocuparán niveles de energía mayores a medida que los niveles inferiores se van llenando.
La energía de Fermi es un concepto que tiene muchas aplicaciones en la teoría del orbital, en el comportamiento de los semiconductores y en la física del estado sólido en general.
En física del estado sólido la superficie de Fermi es la superficie en el espacio de momentos en la que la energía de excitación total iguala a la energía de Fermi. Esta superficie puede tener una topología no trivial. Brevemente se puede decir que la superficie de Fermi divide los estados electrónicos ocupados de los que permanecen libres.
Enrico Fermi y Paul Dirac, derivaron las estadísticas de Fermi-Dirac. Estas estadísticas permiten predecir el comportamiento de sistemas formados por un gran número de electrones, especialmente en cuerpos sólidos.
La energía de Fermi de un gas de Fermi (o gas de electrones libres) no relativista tridimensional se puede relacionar con el potencial químico a través de la ecuación:

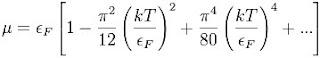
donde εF es la energía de Fermi, k es la constante de Boltzmann y T es la temperatura. Por lo tanto, el potencial químico es aproximadamente igual a la energía de Fermi a temperaturas muy inferiores a una energía característica denominada Temperatura de Fermi, εF/k. Esta temperatura característica es del orden de 105K para un metal a una temperatura ambiente de (300 K), por lo que la energía de Fermi y el potencial químico son esencialmente equivalentes. Este es un detalle significativo dado que el potencial químico, y no la energía de Fermi, es quien aparece en las estadísticas de Fermi-Dirac.

Efectp de Hass - Van Alphen

Efectp de Hass - Van Alphen
Analicemos ahora el comportamiento para temperaturas bajas. Como sabemos, los electrones `intentan' ocupar los estados de energía más baja, aunque también sabemos que a medida que se reduce el valor de B, correspondientemente caben menos en el estado fundamental, porque la degeneración g disminuye linealmente conB. Esto trae como consecuencia oscilaciones en la magnetización, fenómeno que se conoce como efecto de Haas - Van Alphen, a partir de los resultados de un famoso experimento realizado por estos investigadores en 1930, en una muestra de bismuto a 14,2 K entre 0,5 y 2 Tesla.
Al interesarnos en el casoKT<Definiendoμo=eh/(2mc), los niveles de Landau pueden escribirse como ei=2μoB(j+1/2), y en términos de Bo=nhc/e, donde n=N/((L)^2)es el número de partículas por unidad de área, su degeneración es g=NB/Bo. La magnitud Bo representa el valor mínimo para que todos los electrones quepan en cada uno de los niveles de Landau. A T=0, cuando B>Botodos los electrones se acomodan en el nivel fundamental j=0; en ese caso, la energía por partícula será Eo/N=μB. Si en cambio B(1+j)g < N < (1+2)g
es decir

Efecto Hall

Efecto Hall

Anteriormente se creía que el efecto Hall cuántico sólo era apreciable a temperaturas cercanas al cero absoluto. Pero cuando unos científicos del Laboratorio Nacional de Altos Campos Magnéticos en Tallahassee, Florida, del Laboratorio de Electroimanes de Altos Campos en Nijmegen, Países Bajos, y de otras instituciones, colocaron una forma de carbono bastante nueva, el grafeno, en campos magnéticos muy elevados, lo que vieron les asombró.

"Normalmente, a temperatura ambiente, estas ondas de electrones resultan destruidas, y con ellas los efectos cuánticos", explica Horst Stormer, profesor de física en la Universidad de Columbia, galardonado con un Premio Nobel, y uno de los autores del estudio. "Sólo en raras ocasiones este mundo cuántico sobrevive a la escala de temperaturas en que nos movemos los humanos".

Efecto Hall Cuántico

El efecto Hall cuántico es la base para el estándar internacional de resistencia eléctrica empleado para caracterizar los materiales conductores de la electricidad. Fue descubierto en 1980 por el físico alemán Klaus von Klitzing, a quien le fue otorgado un Premio Nobel en 1985 por su descubrimiento. Hasta muy recientemente se consideraba que el efecto Hall cuántico pertenecía al campo de las muy bajas temperaturas.

Sin embargo, esa opinión empezó a cambiar con la posibilidad de producir campos magnéticos muy altos y con el descubrimiento del grafeno, una sola capa de átomos casi tan fuerte como el diamante. Ambos descubrimientos han permitido a los científicos llevar este frágil efecto cuántico hasta la temperatura ambiente. Ahora existe una forma de ver los curiosos y a menudo sorprendentes efectos cuánticos, como el flujo de la corriente sin fricción, con exactitudes de unas pocas partes por millar de millones, incluso a la temperatura ambiente.

La investigación fue llevada a cabo por científicos de los dos laboratorios antedichos, y también de la Universidad de Manchester, la Universidad de Columbia en Nueva York, y la Fundación para la Investigación Fundamental de la Materia en los Países Bajos.

Electron-hueco

Un hueco de electrón , o simplemente hueco*, es la ausencia de un electrón en la banda de valencia (ver también valencia) . Tal banda de valencia estaría normalmente completa sin el "hueco". Una banda de valencia completa ( o casi completa) es característica de los insuladores (también llamados aislantes) y de los semiconductores. La noción de "hueco" en este caso es esencialmente un modo sencillo útil para analizar el movimiento de un gran número de electrones, considerando ex profeso a esta ausencia o hueco de electrones como si fuera una partícula elemental o -más exactamente- una casi-partícula. Considerado lo anterior, el hueco de electrón es, junto al electrón, entendido como uno de los portadores de carga que contribuyen al paso de corriente eléctrica en los semiconductores. El hueco de electrón tiene valores absolutos de la misma carga que el electrón pero, contrariamente al electrón, su carga es positiva. Aunque bien corresponde el recalcar que los huecos no son partículas como sí lo es -por ejemplo- el electrón, sino la falta de un electrón en un semiconductor; a cada falta de un electrón -entonces- resulta asociada una complementaria carga de signo positivo (+). Por ejemplo cuando un cristal tetravalente (es decir de 4 valencias) como el muy conocido silicio es dopado con átomos específicos que, como el boro, poseen sólo tres electrones en estado de valencia atómica, uno de los cuatro enlaces del silicio queda libre. Es entonces que los electrones adyacentes pueden con cierta facilidad desplazarse y ocupar el lugar que ha quedado libre en el enlace; este fenómeno es llamado entonces hueco. Para un observador externo lo antedicho será percibido como el "desplazamiento de una carga positiva", sin embargo lo real es que se trata del desplazamiento de electrones en sentido opuesto al más frecuente. La descripción figurada de un hueco de electrón como si se tratara de una partícula equiparable al electrón aunque con carga eléctrica positiva es en todo caso didácticamente bastante útil al permitir describir el comportamiento de estos fenómenos. Otra característica peculiar de los huecos de electrón es que su movilidad resulta ser menor que la de los electrones propiamente dichos; por ejemplo la relación entre la movilidad de los electrones y la de los huecos(de electrones) tiene un valor aproximado de 2,5-3.